Jingbo Su

Jingbo Su

RA @ UCR PAL

Sequence Models

4 minute read

Published:

RNN, GRU, and LSTM

Recurrent Neural Network (RNN)

  • Problems
    • Various length - Inputs, outputs can be different lengths in different examples.
    • Position information - Doesn’t share features across different positions of text.

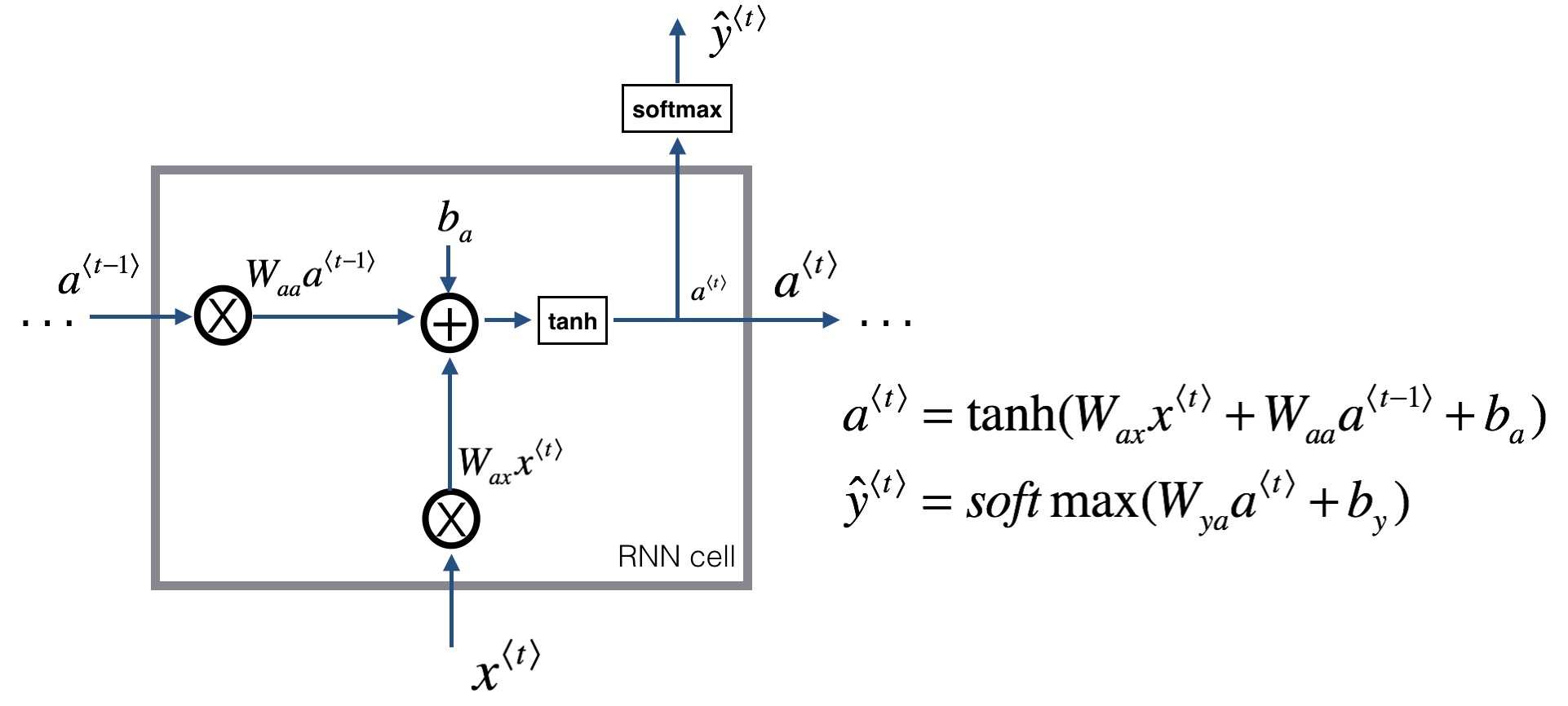
rnn_step_forward

\[\begin{align*} a^{\langle t\rangle}&=\tanh\left(W_{aa}a^{\langle t-1\rangle}+W_{ax}x^{\langle t\rangle}+b_a\right)\\ &=\tanh\left(W_a\left[a^{\langle t-1\rangle},\ x^{\text{t}}\right]+b_a\right)\\ \hat{y}^{\langle t\rangle}&=\text{softmax}\left(W_{ya}a^{\langle t\rangle}+b_y\right) \end{align*}\]

RNN back propagation equations

To compute the rnn_cell_backward you can utilize the following equations. It is a good exercise to derive them by hand. Here, $*$ denotes element-wise multiplication while the absence of a symbol indicates matrix multiplication.

\(\begin{align} a^{\langle t \rangle} = \tanh(W_{ax} x^{\langle t \rangle} + W_{aa} a^{\langle t-1 \rangle} + b_{a})\tag{*}\\ \frac{\partial \tanh(x)} {\partial x} = 1 - \tanh^2(x)\tag{*} \end{align}\) \(\begin{align*} {dW_{ax}} &= da_{next} * ( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) ) x^{\langle t \rangle T}\tag{1}\\ dW_{aa} &= da_{next} * ( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) ) a^{\langle t-1 \rangle T}\tag{2}\\ db_a &= da_{next} * \sum_{batch}( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) )\tag{3}\\ dx^{\langle t \rangle} &= da_{next} * { W_{ax}}^T ( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) )\tag{4}\\ da_{prev} &= da_{next} * { W_{aa}}^T ( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) )\tag{5} \end{align*}\)

Gated Recurrent Unit (GRU)

  • $c$: memory cell
  • $c^{\langle t\rangle}=a^{\langle t\rangle}$
\[\begin{align*} c^{\langle t-1\rangle}&=a^{\langle t-1\rangle}\tag{1}\\ \tilde{c}^{\langle t\rangle}&=\tanh\left(W_c\left[\Gamma_r\cdot c^{\langle t-1\rangle},\ x^{\langle t\rangle}\right]+b_c\right)\tag{2}\\ \Gamma_u&=\sigma\left(W_u\left[c^{\langle t-1\rangle},\ x^{\langle t\rangle}\right]+b_u\right)\tag{3}\\ \Gamma_r&=\sigma\left(W_r\left[c^{\langle t-1\rangle},\ x^{\langle t\rangle}\right]+b_r\right)\tag{4}\\ c^{\langle t\rangle}&=\Gamma_u\cdot \tilde{c}^{\langle t\rangle}+(1-\Gamma_u)\cdot c^{\langle t-1\rangle}\tag{5}\\ a^{\langle t\rangle}&=c^{\langle t\rangle}\tag{6}\\ \hat{y}^{\langle t\rangle}&=\text{softmax}\left(W_{ya}a^{\langle t\rangle}+b_y\right)\tag{7} \end{align*}\]
  • (2) - $\tilde{h}$
  • (3) - $u$
    • $\Gamma_u$ close to 0 $\Rightarrow$ solve grad vanishing
    • $\Gamma_u=1$ $\Rightarrow$ $c^{\langle t\rangle}=\tilde{c}^{\langle t\rangle}$ - update/remember current information
    • $\Gamma_u=0$ $\Rightarrow$ $c^{\langle t\rangle}=c^{\langle t-1\rangle}$ - keep the memory & don’t update
  • (4) - $r$
  • (5) - $h$
  • (7) - $y_{pred}^t$

Long Short Term Memory (LSTM)

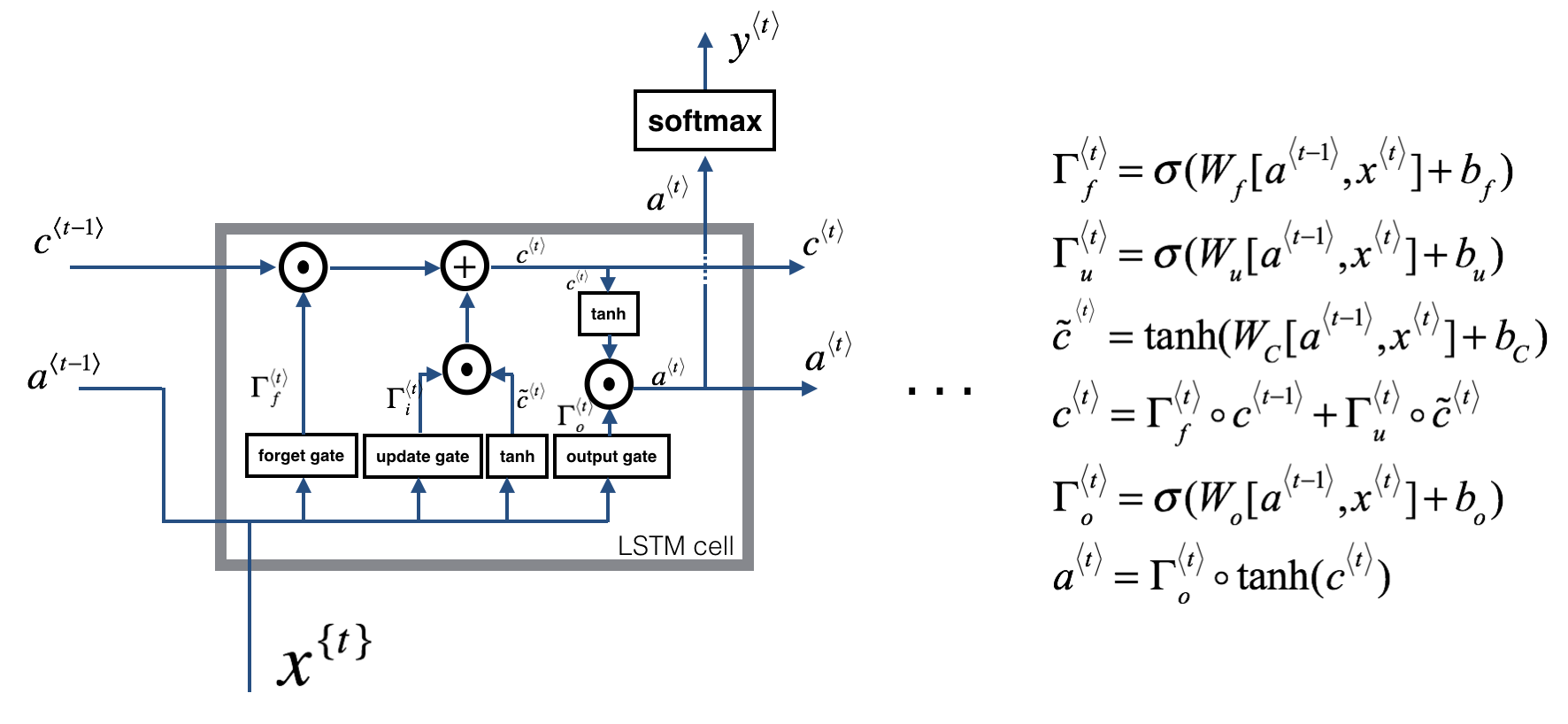
lstm_step_forward

\[\begin{align*} p\tilde{c}^{\langle t\rangle}&=W_c\left[a^{\langle t-1\rangle},\ x^{\langle t\rangle}\right]+b_c\tag{1}\\ \tilde{c}^{\langle t\rangle}&=\tanh\left(p\tilde{c}^{\langle t\rangle}\right)\tag{2}\\ \Gamma_u&=\sigma\left(W_u\left[a^{\langle t-1\rangle},\ x^{\langle t\rangle}\right]+b_u\right)\tag{3}\\ \Gamma_f&=\sigma\left(W_f\left[a^{\langle t-1\rangle},\ x^{\langle t\rangle}\right]+b_f\right)\tag{4}\\ \Gamma_o&=\sigma\left(W_o\left[a^{\langle t-1\rangle},\ x^{\langle t\rangle}\right]+b_o\right)\tag{5}\\ c^{\langle t\rangle}&=\Gamma_u\cdot \tilde{c}^{\langle t\rangle}+\Gamma_f\cdot c^{\langle t-1\rangle}\tag{6}\\ a^{\langle t\rangle}&=\Gamma_o\cdot \tanh \left(c^{\langle t\rangle}\right)\tag{7}\\ z^{\langle t\rangle}&=W_{ya}a^{\langle t\rangle}+b_y\tag{8}\\ \hat{y}^{\langle t\rangle}&=\text{softmax}\left(z^{\langle t\rangle}\right)\tag{9} \end{align*}\]
  • (2) - Update gate
  • (3) - Forget gate
  • (4) - Output gate

*LSTM backward propagation pass

a. gate derivatives

Note the location of the gate derivatives ($\gamma$..) between the dense layer and the activation function (see graphic above). This is convenient for computing parameter derivatives in the next step.

\[\begin{align*} L&=\sum_t^{T_x}\sum_i^{n_y} -y_i^{\langle t\rangle}\log\hat{y_i^{\langle t\rangle}}\tag{10}\\ &\frac{\partial L}{\partial z^{\langle t\rangle}}=\hat{y}^{\langle t\rangle}-y^{\langle t\rangle}\tag{11}\\ \bullet\ a^{\langle t\rangle}\text{ impacts } y^{\langle t\rangle}\text{ and }y^{\langle t+1\rangle}:\\ \frac{\partial L}{\partial a^{\langle t\rangle}}&=\frac{\partial L^{\langle t\rangle}}{\partial a^{\langle t\rangle}}+\frac{\partial L^{\langle t+1\rangle}}{\partial a^{\langle t\rangle}}\\ &=\frac{\partial L^{\langle t\rangle}}{\partial z^{\langle t\rangle}}\frac{\partial z^{\langle t\rangle}}{\partial a^{\langle t\rangle}}+\frac{\partial L^{\langle t+1\rangle}}{\partial a^{\langle t\rangle}}\\ &=W_{ya}^T\left(\hat{y^{\langle t\rangle}}-y^{\langle t\rangle}\right)+da_{next}\tag{12}\\ \bullet\ c^{\langle t\rangle}\text{ impacts }c_{next}\text{ and }a^{\langle t\rangle}:\\ \frac{\partial L}{\partial c^{\langle t\rangle}}&=\frac{\partial L^{\langle t\rangle}}{\partial c^{\langle t\rangle}}+\frac{\partial L^{\langle t+1\rangle}}{\partial c^{\langle t\rangle}}\\ &=\frac{\partial L^{\langle t\rangle}}{\partial a^{\langle t\rangle}}\frac{\partial a^{\langle t\rangle}}{\partial c^{\langle t\rangle}}+\frac{\partial L^{\langle t+1\rangle}}{\partial c^{\langle t\rangle}}\\ &=\frac{\partial L^{\langle t\rangle}}{\partial a^{\langle t\rangle}}\Gamma_o\left(1-\tanh^2 c^{\langle t\rangle}\right)+dc_{next}\\ &=da_{next}\cdot\Gamma_o\left(1-\tanh^2 c^{\langle t\rangle}\right)+dc_{next}\tag{13}\\ \frac{\partial L}{\partial \tilde{c}^{\langle t\rangle}}&=\frac{\partial L}{\partial c^{\langle t\rangle}}\frac{\partial c^{\langle t\rangle}}{\partial\tilde{c}^{\langle t\rangle}}\\ &=\frac{\partial L}{\partial c^{\langle t\rangle}}\Gamma_u^{\langle t\rangle}\tag{14}\\ \frac{\partial L}{\partial p\tilde{c}^{\langle t\rangle}}&=\frac{\partial L}{\partial\tilde{c}^{\langle t\rangle}}\frac{\partial\tilde{c}^{\langle t\rangle}}{\partial p\tilde{c}^{\langle t\rangle}}\\ &=\frac{\partial L}{\partial\tilde{c}^{\langle t\rangle}}\left(1-\tanh^2p\tilde{c}^{\langle t\rangle}\right)\\ &=\frac{\partial L}{\partial\tilde{c}^{\langle t\rangle}}\left[1-\left(\tilde{c}^{\langle t\rangle}\right)^2\right]\tag{15}\\ \bullet\text{ Update gate}\\ \frac{\partial L}{\partial\gamma_u^{\langle t\rangle}}&=\frac{\partial L}{\partial c^{\langle t\rangle}}\frac{\partial c^{\langle t\rangle}}{\partial\Gamma_u^{\langle t\rangle}}\frac{\partial\Gamma_u^{\langle t\rangle}}{\partial\gamma_u^{\langle t\rangle}}\\ &=\frac{\partial L}{\partial c^{\langle t\rangle}}\cdot\tilde{c}^{\langle t\rangle}\cdot\Gamma_u^{\langle t\rangle}\left(1-\Gamma_u^{\langle t\rangle}\right)\tag{16}\\ \bullet\text{ Forget gate}\\ \frac{\partial L}{\partial\gamma_u^{\langle t\rangle}}&=\frac{\partial L}{\partial c^{\langle t\rangle}}\frac{\partial c^{\langle t\rangle}}{\partial\Gamma_f^{\langle t\rangle}}\frac{\partial\Gamma_f^{\langle t\rangle}}{\partial\gamma_f^{\langle t\rangle}}\\ &=\frac{\partial L}{\partial c^{\langle t\rangle}}c_{prev}\cdot\Gamma_f^{\langle t\rangle}\left(1-\Gamma_f^{\langle t\rangle}\right)\tag{17}\\ \bullet\text{ Output gate}\\ \frac{\partial L}{\partial\gamma_o^{\langle t\rangle}}&=\frac{\partial L}{\partial a^{\langle t\rangle}}\frac{\partial a^{\langle t\rangle}}{\partial\Gamma_o^{\langle t\rangle}}\frac{\partial\Gamma_o^{\langle t\rangle}}{\partial\gamma_o^{\langle t\rangle}}\\ &=\frac{\partial L}{\partial a^{\langle t\rangle}}\tanh c^{\langle t\rangle}\cdot\Gamma_o^{\langle t\rangle}\left(1-\Gamma_o^{\langle t\rangle}\right)\tag{18} \end{align*}\]

b. parameter derivatives

\[\begin{align*} dW_f = d\gamma_f^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{19}\\ dW_u = d\gamma_u^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{20}\\ dW_c = dp\widetilde c^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{21}\\ dW_o = d\gamma_o^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{22} \end{align*}\]

To calculate $db_f, db_u, db_c, db_o$ you just need to sum across the horizontal (axis=1) axis on $d\gamma_f^{\langle t \rangle}, d\gamma_u^{\langle t \rangle}, dp\widetilde c^{\langle t \rangle}, d\gamma_o^{\langle t \rangle}$ respectively. Note that you should have the keepdims=True option.

\[\begin{align*} db_f = \sum_{batch}d\gamma_f^{\langle t \rangle}\tag{23}\\ db_u = \sum_{batch}d\gamma_u^{\langle t \rangle}\tag{24}\\ db_c = \sum_{batch}d\gamma_c^{\langle t \rangle}\tag{25}\\ db_o = \sum_{batch}d\gamma_o^{\langle t \rangle}\tag{26} \end{align*}\]

Finally, you will compute the derivative with respect to the previous hidden state, previous memory state, and input.

\[\begin{align*} da_{prev}&=\frac{\partial L}{\partial a^{\langle t-1\rangle}}\\ &=\frac{\partial L}{\partial p\tilde{c}^{\langle t\rangle}}\frac{\partial p\tilde{c}^{\langle t\rangle}}{\partial a^{\langle t-1\rangle}}+\frac{\partial L}{\partial\gamma_u^{\langle t\rangle}}\frac{\partial\gamma_u^{\langle t\rangle}}{\partial a^{\langle t-1\rangle}}+\frac{\partial L}{\partial\gamma_f^{\langle t\rangle}}\frac{\partial\gamma_f^{\langle t\rangle}}{\partial a^{\langle t-1\rangle}}+\frac{\partial L}{\partial\gamma_o^{\langle t\rangle}}\frac{\partial\gamma_o^{\langle t\rangle}}{\partial a^{\langle t-1\rangle}}\\ &=W_{ca}^T\frac{\partial L}{\partial p\tilde{c}^{\langle t\rangle}}+W_{ua}^T\frac{\partial L}{\partial \gamma_u^{\langle t\rangle}}+W_{fa}^T\frac{\partial L}{\partial\gamma_f^{\langle t\rangle}}+W_{oa}^T\frac{\partial L}{\partial\gamma_o^{\langle t\rangle}}\\ &=W_c^T dp\widetilde c^{\langle t \rangle}+W_u^T d\gamma_u^{\langle t \rangle}+W_f^T d\gamma_f^{\langle t \rangle}+W_o^T d\gamma_o^{\langle t \rangle}\tag{27} \end{align*}\]

Here, to account for concatenation, the weights for equations 28 are the first $n_a$, (i.e. $W_f = W_f[:,:n_a]$ etc…)

\[\begin{align*} dc_{prev}&=\frac{\partial L}{\partial c^{\langle t-1\rangle}}\\ &=\frac{\partial L}{\partial c^{\langle t\rangle}}\frac{\partial c^{\langle t\rangle}}{\partial c^{\langle t-1\rangle}}\\ &=\frac{\partial L}{\partial c^{\langle t\rangle}}\Gamma_f^{\langle t\rangle}\\ &=dc_{next}*\Gamma_f^{\langle t \rangle} + \Gamma_o^{\langle t \rangle} * (1- \tanh^2(c_{next}))*\Gamma_f^{\langle t \rangle}*da_{next}\tag{28} \end{align*}\]

Comparison

  • GRU: simple & faster
  • LSTM: powerful & flexible